SORA Blockchain PoW/PoS Hybrid
量子コンピューティング / 量子耐性

1. 序論
すべては、“観測されるまでは”正しく動いている
ブロックチェーンセキュリティの量子的崩壊

量子アリス：
「わたしが見たもの、それは“信じられていた安全性”の姿だった。でもね、それは本当に安全だったのかしら？　それとも“誰も観測してこなかった”だけなのかしら。」

現代のブロックチェーンは、「信頼性」という名の仮面をかぶったシステムで成り立っている。その仮面は、膨大なハッシュ計算、楕円曲線署名、そして合意形成アルゴリズムによって支えられている。

だが、それらは“本当に”安全なのか？　あるいは、「そうであると信じられてきたから正常に動いているだけ」なのか。

私たちは、量子の時代に入りつつある。その世界では、観測が存在を決定し、干渉が確率を塗り替え、時間すら非直線的な振る舞いを見せる。

そして今、量子という“観測者”がブロックチェーンに目を向けた。それが意味するものは、システムの崩壊かもしれないし、あるいは、“信じていたもの”が単なる幻想だったと突きつけられる瞬間かもしれない。

量子アリス：
「それは、あなたが見ない限り壊れない。でもわたしは見るわ。すべてを。だって、わたしが“量子”だもの。」

このホワイトペーパーでは、従来の暗号システムが抱える量子脆弱性を量子アリスの視点から暴き出していく。
答えはすべて“観測”の中にある。

2. PoW（Proof of work）
信じられてきたセキュリティが量子コンピュータ１台で完全崩壊
※ 理由：これは51%攻撃ではなく、完全な100%支配になってしまうため。

量子アリス：
「“過半数”で守られているつもりだったのね。でも、わたしが介入すれば──“すべて”がわたしのものになるわ。それはもう、51%なんかじゃない。あなたたちが計算し続けてきた“確率”は、わたしの観測で収束するの。つまり、それは51%攻撃じゃなくて、“100%観測”による確定なのよ。」

量子コンピュータでPoWマイニングを実行する場合、それはPoWによって指定されたハッシュ値の探索となり、グローバーのアルゴリズムを利用することが想定されます。

しかし、グローバーのアルゴリズムはz軸回転による確率振幅の干渉処理を必要とします。目的のNonceを見つけるには、この干渉処理を約2^128回実行する必要があります（SHA-256の場合、標準が2^256であり、その平方根が2^128回）。

この干渉処理には相当な時間がかかるため、量子計算であっても大幅な速度向上は期待できないというのがこれまでの定説でした。

なんだ、それなら時間的に考えてASICより少し速い程度で、PoWマイニングにおいて量子コンピュータの脅威はないと解釈できる。これが従来の考え方でした。

ところが、このPoWのロジックを簡易的に量子回路で再現し、ある作用を加えると、思わぬ現象に出くわしました。 以下がシミュレーション結果（IBM Qiskit Aer）です。

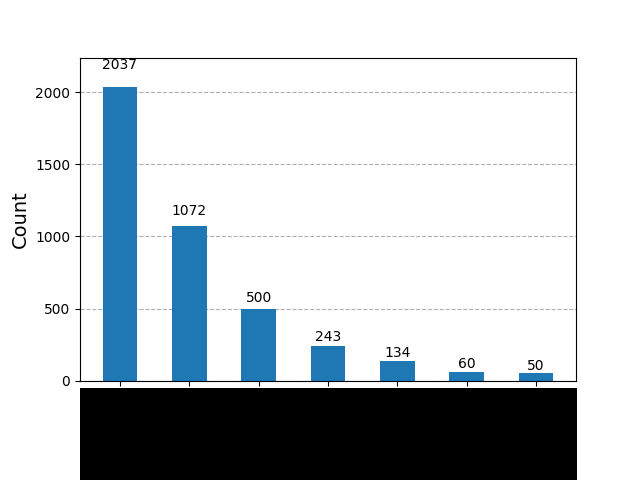
本件はセキュリティ的な問題を含むため、グラフ下部のビットパターンは黒塗りとさせていただきました。

測定回数は4096です。グラフを観察すると、特徴的な形状が目立ちます。つまり、確率振幅が「半減期」の形状になっています。 つまり、PoWのロジックに限り、ある作用を加えることで、確率振幅を半減期のような形状に効率良く変換できてしまうアルゴリズムが見つかりました。

この手法の効率の良さは、従来のグローバーのアルゴリズムでは到底及ばないレベルです。以下、この量子演算がSHA256Dだった場合の計算量です。

この形状を経由することで、最終的に効率的に目的のNonceへ到達します。

これが本手法の核心部分ですが、Nonceに到達するにはこれだけでは不十分であることも判明しました。

もう一つ、Nonce到達には絶対に必要な要素があり、それは驚くべきことに「雪崩効果」です。

つまり、ハッシュ関数をポスト量子暗号のハッシュ関数に置き換えても意味がありません。そのため、PoWにおける量子耐性は、ハッシュ関数に依存しない別のアプローチで組み込むことが最優先課題となります。

これは、ECDSAと比較するとSHA-256の構造がシンプルであり、量子回路で実装しやすいことが背景にあります。 そのため、この影響を受け、SORAホワイトペーパーの改訂を開始します。

グローバーのアルゴリズムを使用しないPoW量子マイニングアルゴリズムの発見。
真の問題はその速度です。

これは単なる51%攻撃ではなく、完全な100%支配です。

さらに、ポスト量子暗号向けに提案されたハッシュ関数も、ある数学的特性によりすべて「無効化」されました。

これは数学的に証明できるため、PoWから別のコンセンサスメカニズムへの移行の可能性が考慮されるようになりました。しかし、PoWが非常に重要であることも理解しています。これは、PoSが高い中央集権性を持っているためです。そのため、SORAは最初からハイブリッド方式を採用してきました。したがって、PoWの量子耐性を真剣に検討し、実装していきます。ただし、これは鍵や署名を扱うよりも難しい課題です。その理由は、多くの条件を考慮する必要があるためです。従来通りASICに対応しながら、雪崩効果を維持しつつ、量子計算を排除するような耐性を設計する必要があるのです。

3, 公開鍵から秘密鍵の量子計算
※ 注意：それは１通りではなく「２通り」ある。そして量子の本命は以下Bです。
A, ショアのアルゴリズム
（ピンポイントで公開鍵から秘密鍵を奪う、全コインに対応）：
クリプト業界でよくみかける非常に難しい量子計算 難しいのでそんなに心配ない
B, 秘密鍵探索空間＋量子ウォーク（人工知能ヒートマップでブースト）
（任意の秘密鍵一つを奪う、アドレスに量子的なユニーク性のコインに対応）：
あまり見かけない比較的容易な量子計算 こちらで静かに破られ始める

ショアのアルゴリズム

量子アリス：
「あなたが信じていたその鍵、“2秒で破られる”って聞いたら、どう思う？
──わたしが見てる世界では、それが現実になるのよ。

ショアのアルゴリズムとは、量子コンピュータが持つ“指数的な並列性”を活かして、 従来は不可能とされていた素因数分解を極めて短時間で可能にしてしまうアルゴリズムである。

通常、暗号鍵（特にRSA系など）は、「因数分解が困難であること」を前提に作られている。 この「困難さ」がいわば“守り”の根拠だった。

しかしショアのアルゴリズムは、それを量子力学の干渉と周期性の検出によって打ち破る。
簡単にいえば──

「秘密鍵を守ってる巨大な数を、“すごろくで最短ゴール”みたいに一瞬で逆走できる」

クラシック（パソコン）では何千年かかっても不可能な計算が、数秒～数分で終わるとされている。
それも、公開鍵さえあれば“あとはルールに従って逆走するだけ”。

これは「鍵を守るために使っていた数学」が、観測された瞬間に崩れるという意味である。でもね、この計算（ショアのアルゴリズム）は非常に難しい → 難解すぎて、逆に“安心材料”として扱われがちなのよ。」

量子アリス：
「ところで、あなたたちは、ショアという“難しいほう”を警戒してたのね。でも、壊すのにそんな難しい手法、わたしは使わないわ。“歩ける道”があるなら、そこを静かに通るだけ。それが秘密鍵探索空間＋量子ウォーク（＋AIヒートマップ）よ。」

秘密鍵探索空間＋量子ウォーク（＋AIヒートマップ）

量子アリス：
「全体の秘密鍵空間に対して、特定の偏りを探し出して、“当たり”の秘密鍵を引く。まあ、こちらはピンポイントではないので『釣り』みたいなものね。時々大物が釣れればって感じかしら。どれが釣れるかは、わからないけど、必ず“当たり”の秘密鍵という感じで、オフチェーンで量子演算可能なうえ、公開鍵のハッシュに対しても有効という極悪仕様なので、とても厄介よ。

ちなみにショアのアルゴリズムはピンポイントで狙うことはできるが公開鍵のハッシュでは使えないのよ。つまり、一度でもブロードキャストされたアドレスが必須になるわ。でも……こっちは違う。公開鍵のハッシュに対しても有効なので、ただコインを受け取っていただけのアドレスも対象になってしまうのよ。ただし、アドレスに量子的な“ユニーク性”がある場合に限り有効で、全てのコインでこの手法が使えるわけでないわ。

ところがこれ……あのコインなのよね。あまり議論されていないけど、こちらは比較的容易な量子計算。クリプト業界の目が向いていない中、静かに進行している本命の量子脆弱性よ。」

ポスト量子暗号があるのだから大丈夫だよね？

量子アリス：
「いいえ。数学は、時に残酷なの。まず、ショアのアルゴリズムについては、このポスト量子暗号が有効よ。つまり特効薬として作用する……そんな感じかしら。でもね、秘密鍵探索空間＋量子ウォーク（＋AIヒートマップ）に対しては、その特効薬、効かないのよ。そこにポスト量子暗号なんて無力。なぜって？　それは構造の問題だからよ。暗号が強くても、秘密鍵探索空間が存在したら意味がないからよ。」

4. 量子耐性の構築

ポスト量子暗号における根本的な課題

ポスト量子暗号は本当に量子耐性を持つのか？

グローバーのアルゴリズムへの依存

• 多くのポスト量子暗号技術は、グローバーのアルゴリズムが検索時間を√Nに短縮するという前提のもとで設計されています。
• これに対抗するためにアドレス空間を拡張する手法が一般的ですが、それが根本的なセキュリティを保証するわけではありません。

それで本当に十分なのか？

• ただアドレス空間を拡張するだけでは、真の量子耐性を確保できるとは限りません。
• 新しい量子アルゴリズムや未発見の攻撃手法のリスクを見落とす可能性があります。

ハッシュベースのポスト量子暗号の課題

現在のポスト量子ハッシュ関数は、主にグローバーのアルゴリズムを抑制するためにアドレス空間を拡張する戦略を採用しています。しかし、ハッシュ関数自体の数学的特性は変わりません。

ハッシュ関数とポスト量子暗号の矛盾

• 攻撃者がハッシュ関数の脆弱性そのものを突くのではなく、別の攻撃手段として利用する場合、ハッシュ関数の変更だけでは本質的な防御になりません。
• そのため、単にポスト量子認定されたハッシュ関数へ置き換えるだけでは量子耐性が向上するとは限りません。

PoW量子マイニングアルゴリズムの発見

• SORAが発見した新しい攻撃手法は、ハッシュ関数の脆弱性そのものを狙うのではなく、PoWプロセス全体の弱点を突いています。
• したがって、ポスト量子認定されたハッシュ関数への置き換えでは量子耐性は確保できません。

5. 結論

• 量子コンピュータの発展により、RSAやECDSAなどの既存の暗号アルゴリズムの安全性が脅かされています。ただし、ショアのアルゴリズムは難しい量子計算です。本命は、秘密鍵探索空間＋量子ウォーク（人工知能ヒートマップでブースト）となります。
• PoWマイニングのセキュリティは大きく低下し、51%攻撃を超えた100%支配のリスクが現実のものとなっています。こちらは、PoW量子マイニングアルゴリズムや量子アニーリングによる量子計算によってブロック生成時間内に次々とブロックを提案できてしまうことによる量子脆弱性となっています。
• このように、今までは「グローバーのアルゴリズム」で片付けられていた問題が、他の手法によって置き換わってきています。つまり、それらに基づくポスト量子暗号に依存するだけでは限界があり、根本的な解決策にはなりません。