SORA Blockchain PoW/PoS Hybrid
Quantum-computing / Quantum-resistant

1. Introduction
Everything Works Until It’s Observed
The Quantum Collapse of Blockchain Security

Quantum Alice:
“What I saw... was the form of so-called ‘trusted security.’ But was it ever truly secure? Or was it merely never observed?”

Modern blockchains operate under the mask of something called “trust.” That mask is held in place by massive hash computations, elliptic curve signatures, and consensus algorithms.

But are these systems truly “secure”? Or do they only appear functional because we’ve simply believed they are?

We are now entering the quantum age- a world where observation defines existence, interference reshapes probabilities, and even time behaves non-linearly.

And now, the observer called “quantum” has turned its gaze to the blockchain. This may mark the collapse of entire systems- or the moment we’re forced to accept that what we believed in was nothing but illusion.

Quantum Alice:
“Nothing breaks-until you observe it. But I will observe it. All of it. Because I am quantum.”

In this whitepaper, we will reveal the quantum vulnerabilities of legacy cryptographic systems through the eyes of Quantum Alice.
The answers lie within observation.

2. PoW (Proof of Work)
Security once believed to be absolute-shattered by a single quantum computer
* Why? Because this is not a 51% attack. It's 100% control.

Quantum Alice:
“You thought majority control could protect you. But once I intervene everything becomes mine. This isn’t 51%. The probabilities you’ve endlessly calculated… collapse at the moment I observe them. This isn’t a 51% attack. This is 100% certainty through observation.”

When executing PoW mining with a quantum computer, it involves searching for the hash value specified by PoW, which is assumed to utilize Grover's algorithm.

However, Grover's algorithm requires an interference process of probability amplitudes caused by rotation along the z-axis. To find the target Nonce, this interference process must be executed approximately 2^128 times (in the case of SHA-256, the standard is 2^256, and its square root results in 2^128 times).

Because this interference process takes a considerable amount of time, it has been a prevailing theory that, even with quantum computation, a significant speed improvement cannot be expected.

What? In that case, considering the time aspect, it would only be slightly faster than an ASIC, so it could be interpreted that quantum computers do not pose a threat to PoW mining. That was the conventional way of thinking.

However, when we reproduced this PoW logic in a simplified form using a quantum circuit and applied a certain effect, we encountered an unexpected phenomenon. The following is the simulation result (IBM Qiskit Aer).

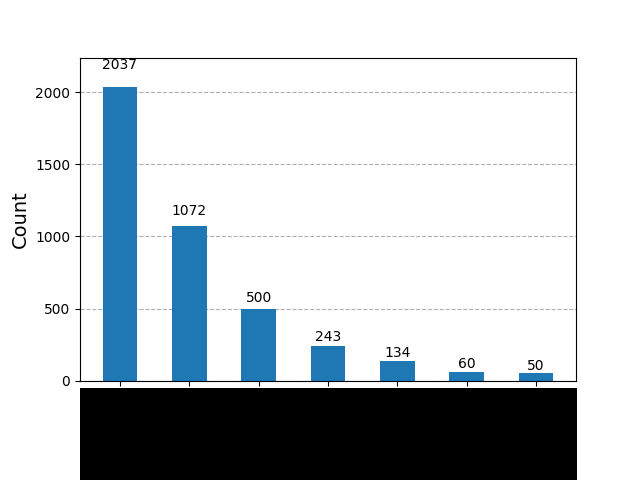
Since this matter involves security concerns, the bit pattern at the bottom of the graph has been blacked out.

The number of measurements is 4096. When observing the graph, the distinctive shape immediately stands out. In other words, the probability amplitude takes on the shape of a "half-life" curve. This means that, specifically for PoW logic, we have discovered an algorithm that can efficiently transform the probability amplitude into a half-life-like shape by applying a certain effect.

The efficiency of this method is far beyond what Grover's algorithm can achieve. Below is the computational complexity if this quantum computation were applied to SHA256D.

By passing through this shape, it ultimately reaches the target Nonce efficiently.

That is the core aspect of this discovered algorithm. However, it has also been found that this alone is not sufficient to reach the Nonce.

There is one more absolutely essential element for reaching the Nonce, and surprisingly, it is the "avalanche effect," which is directly related to the security of the hash.

Therefore, even if the hash function is replaced with a post-quantum cryptographic hash function, it is meaningless. For this reason, the top priority is to incorporate quantum resistance into PoW through an alternative approach that does not rely on the hash function.

This is because, compared to ECDSA, the structure of SHA-256 is simpler and easier to implement in a quantum circuit. Furthermore, due to this impact, we will begin the SORA White Paper based on these observations.

A PoW quantum mining algorithm that does not use Grover’s algorithm has been discovered. The real problem is its speed.

This isn’t just a 51% attack - it's a complete 100% takeover.

Furthermore, the hash functions proposed for post-quantum cryptography have all been rendered "invalid" due to a certain mathematical property.

Since this can be mathematically proven, the possibility of transitioning from PoW to an alternative consensus mechanism has now come into consideration. However, we also understand that PoW is extremely important. This is because PoS has a high degree of centralization.For this reason, SORA has adopted a hybrid approach from the very beginning. Thus, we will seriously consider and implement quantum resistance for PoW. However, this is a more difficult challenge than dealing with keys and signatures. The reason is that there are many conditions to consider. It is necessary to ensure compatibility with ASICs as usual while maintaining the avalanche effect and designing a resistance mechanism that excludes quantum computing.

3. Quantum Algorithms for Recovering Private Keys from Public Keys
Note: There are not just one, but two approaches. And the real threat lies in method B.
A. Shor's Algorithm
(Pinpoint extraction of private keys from public keys - applicable to all coins):
A frequently mentioned but extremely complex quantum algorithm in the crypto industry. It's so hard, people aren't too worried.
B. Private Key Search Space + Quantum Walk (boosted by AI Heatmaps)
(Targeting any one private key - applicable to coins with quantum-unique address properties):
A less-discussed, relatively easier quantum computation. This is where things start to quietly fall apart.

Shor's Algorithm

Quantum Alice:
“What would you say if I told you the key you trusted could be broken in two seconds?
In my world… that’s just how it works.”

Shor’s algorithm is a quantum algorithm that uses the “exponential parallelism” of quantum computers to perform what was once considered impossible: factoring large integers in extremely short time.

Traditional cryptographic keys (especially RSA-type) are based on the assumption that “factoring is hard.” That assumption has been the “foundation of security.”

But Shor’s algorithm breaks that foundation using quantum interference and period finding.
Put simply:

“It’s like finding the shortest path backwards on a giant game board that was supposed to be one-way only.”

A computation that would take a classical computer thousands of years can be done in seconds to minutes with quantum computing.
All you need is the public key - from there, it’s just a matter of following the rules backwards.

In other words, the math you used to defend the key collapses the moment it is observed.
But this particular attack (Shor’s algorithm) is extremely difficult - so difficult that it ironically serves as a source of false reassurance.

Quantum Alice:
“So you were worried about Shor - the difficult one. But I don’t use something that complex to break things.
If there’s a path I can walk, I’ll take it quietly.
That’s what the Private Key Search Space + Quantum Walk (with AI Heatmap) is.”

Private Key Search Space + Quantum Walk (with AI Heatmap)

Quantum Alice:
“Across the entire private key space, I look for specific biases - and pull out a ‘winning’ key. It’s not pinpointed like Shor, so think of it like ‘fishing.’ Sometimes you land a big one. You don’t know exactly which, but you know you’ll catch something.
This technique works off-chain, and even applies to hashes of public keys. That makes it far more dangerous.”

By contrast, Shor’s algorithm can only target public keys, not their hashed forms. So it only applies if the address has broadcasted its public key.
But this method? It even works against addresses that merely received coins, as long as they have quantum-unique structural patterns.
Not every coin falls into this category - but...

...that coin does.
It’s not widely discussed, but this method is relatively easy in the quantum world. While the crypto industry is fixated on Shor, this one is quietly proceeding underneath it all. It is the real quantum vulnerability.”

Isn’t Post-Quantum Cryptography Supposed to Protect Us?

Quantum Alice:
“No. Math can be cruel.
Sure, for Shor’s algorithm, post-quantum cryptography acts like a kind of antidote - a special medicine, if you like.
But for Private Key Search Space + Quantum Walk (with AI Heatmap), that antidote doesn’t work.
Post-quantum cryptography is powerless here. Why? Because this isn’t about encryption - it’s about structure. Even if the encryption is strong, if the exploitable space exists, it’s game over.”

4. Building Quantum Resistance

Fundamental Issues in Post-Quantum Cryptography

Is post-quantum cryptography truly quantum-resistant?

Dependence on Grover’s Algorithm

• Many post-quantum cryptographic techniques are designed under the assumption that Grover’s algorithm reduces search time to √N.
• Expanding the address/key space is a common countermeasure, but it does not fundamentally guarantee security.

Is That Really Enough?

• Simply enlarging the address space does not necessarily ensure true quantum resistance.
• There is a risk of overlooking newly developed quantum algorithms or yet undiscovered attack vectors.

Challenges of Hash-Based Post-Quantum Cryptography

Current post-quantum hash functions primarily adopt strategies to suppress Grover’s algorithm by expanding the address space. However, the mathematical properties of the hash functions themselves remain unchanged.

The Inconsistency Between Hash Functions and Post-Quantum Cryptography

• If an attacker leverages the hash function not by exploiting its inherent weaknesses, but as part of an alternative attack route, changing the hash function alone does not provide fundamental defense.
• Therefore, simply replacing a function with a “post-quantum certified” hash function does not necessarily improve quantum resistance.

Discovery of PoW-Based Quantum Mining Algorithms

• The new attack method discovered by SORA targets not the hash function itself, but vulnerabilities in the overall PoW process.
• As a result, replacing the hash function with a post-quantum certified one does not guarantee quantum security.

5. Conclusion

• With the advancement of quantum computers, the security of traditional cryptographic algorithms such as RSA and ECDSA is being challenged. While Shor’s algorithm remains difficult to execute, the true threat lies in Private Key Search Space + Quantum Walk (boosted by AI heatmaps).
• The security of PoW mining has significantly deteriorated, and the risk of 100% control-surpassing even the 51% attack-has become a real concern. This vulnerability arises from the ability to use quantum algorithms like quantum annealing to propose multiple valid blocks within the block time window.
• Thus, what used to be dismissed under the blanket of “Grover’s algorithm” is now being actively replaced by alternative techniques. Sole reliance on post-quantum cryptography based on Grover’s assumptions is insufficient, and it does not represent a fundamental solution.